Explanation Groves

Analyzing the Trade-off between Complexity and Adequacy of Machine Learning Model Explanations

Gero Szepannek, Stralsund University of Applied Sciences

13-05-2025

Machine Learning

James et al. (2019) Fernández-Delgado et al. (2014)

Boston Housing Data

• Harrison and Rubinfeld (1978)

'data.frame':   506 obs. of  16 variables:
 $ lon    : num  -71 -71 -70.9 -70.9 -70.9 ...
 $ lat    : num  42.3 42.3 42.3 42.3 42.3 ...
 $ cmedv  : num  24 21.6 34.7 33.4 36.2 28.7 22.9 22.1 16.5 18.9 ...
 $ crim   : num  0.00632 0.02731 0.02729 0.03237 0.06905 ...
 $ zn     : num  18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
 $ indus  : num  2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
 $ chas   : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 1 ...
 $ nox    : num  0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
 $ rm     : num  6.58 6.42 7.18 7 7.15 ...
 $ age    : num  65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
 $ dis    : num  4.09 4.97 4.97 6.06 6.06 ...
 $ rad    : int  1 2 2 3 3 3 5 5 5 5 ...
 $ tax    : int  296 242 242 222 222 222 311 311 311 311 ...
 $ ptratio: num  15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
 $ b      : num  397 397 393 395 397 ...
 $ lstat  : num  4.98 9.14 4.03 2.94 5.33 ...

• 80:20 Split in training and validation data.

Two Models…

• Decision Tree (rpart, Therneau and Atkinson 2015)…
• …vs. RF (ranger, Wright and Ziegler 2017).
• No HPT as RFs are quite insensitive to tuning (Probst, Boulesteix, and Bischl 2021; Szepannek 2017).
• Result:

	Tree	Forest
Test R²	0.821	0.867

Interpretation Tree Model…

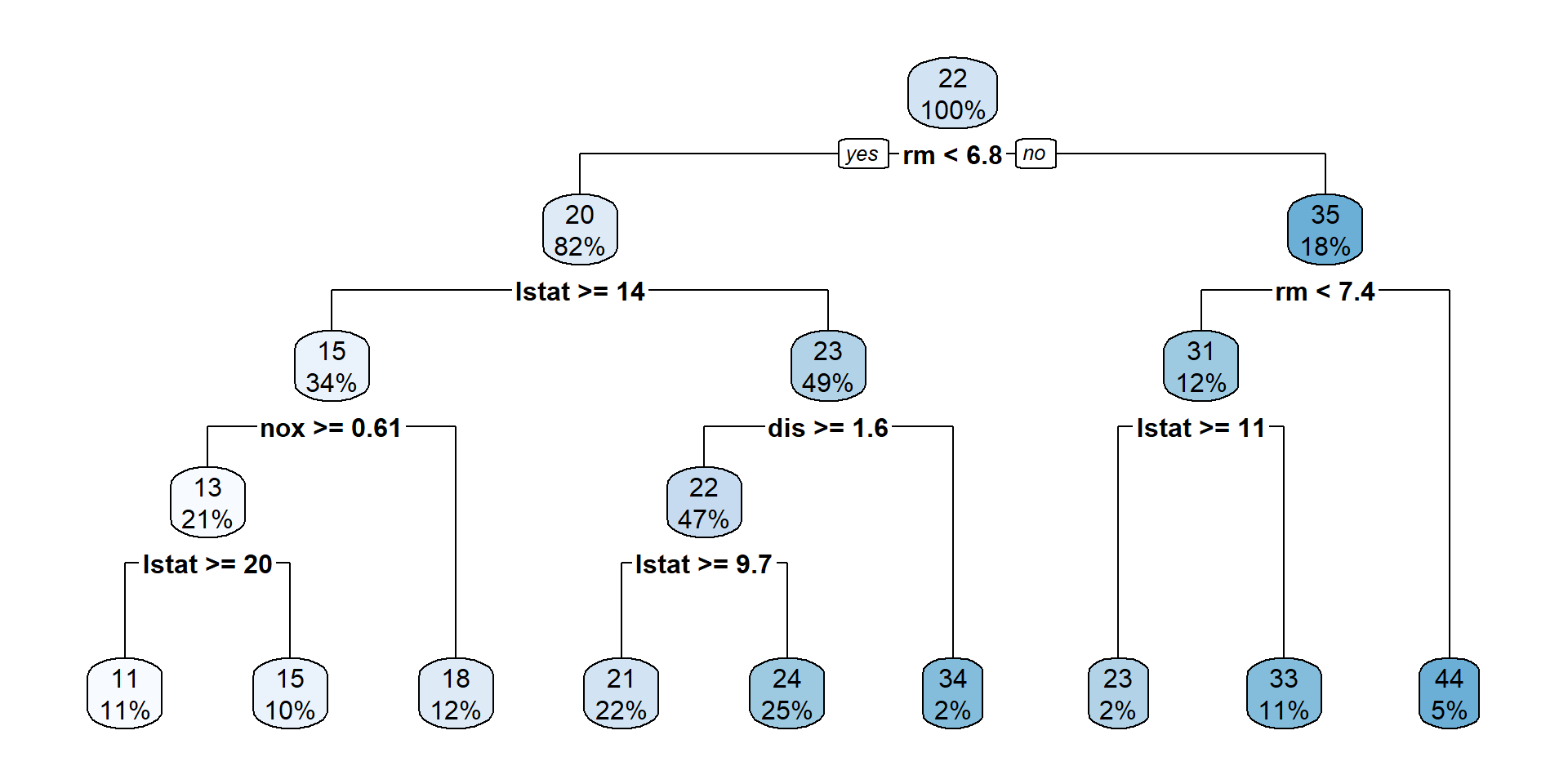
…Interpretation Forest Model

• Number of rules:

	Tree	Forest
# rules	8	65120

• Forest better but no longer interpretable due to large number of rules!
• Two cultures of statistical modelling (Breiman 2001)

Background

• European Commission (2024): EU AI Act
• Bücker et al. (2021): TAX4CS framework
• Molnar et al. (2022): pitfalls
• Gosiewska and Biecek (2019): additivity
• Woźnica et al. (2021): importance of context
• Rudin (2019): use interpretable models instead
• Szepannek and Lübke (2022): analyzing limits of interpretability

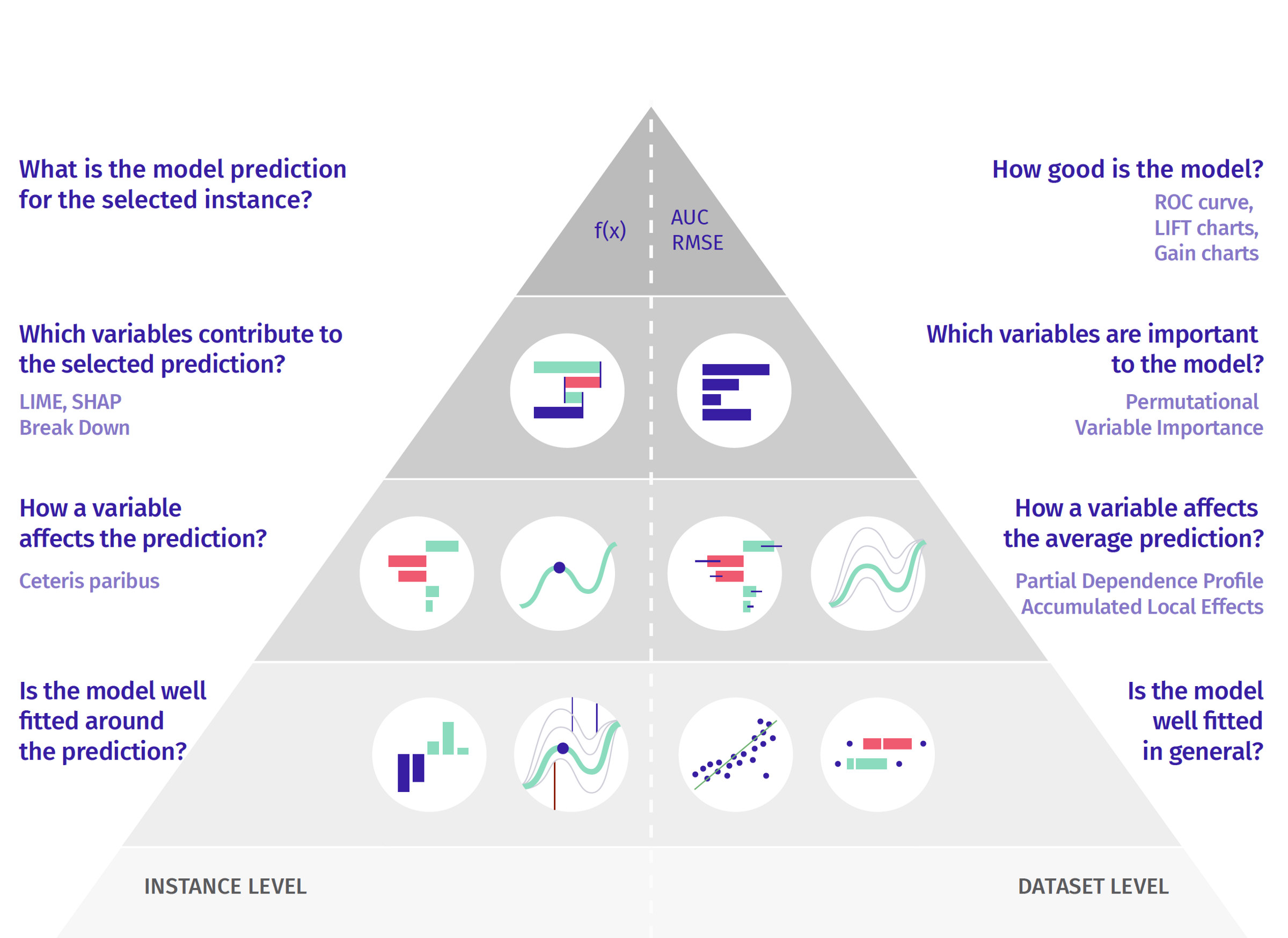
Variable Importance

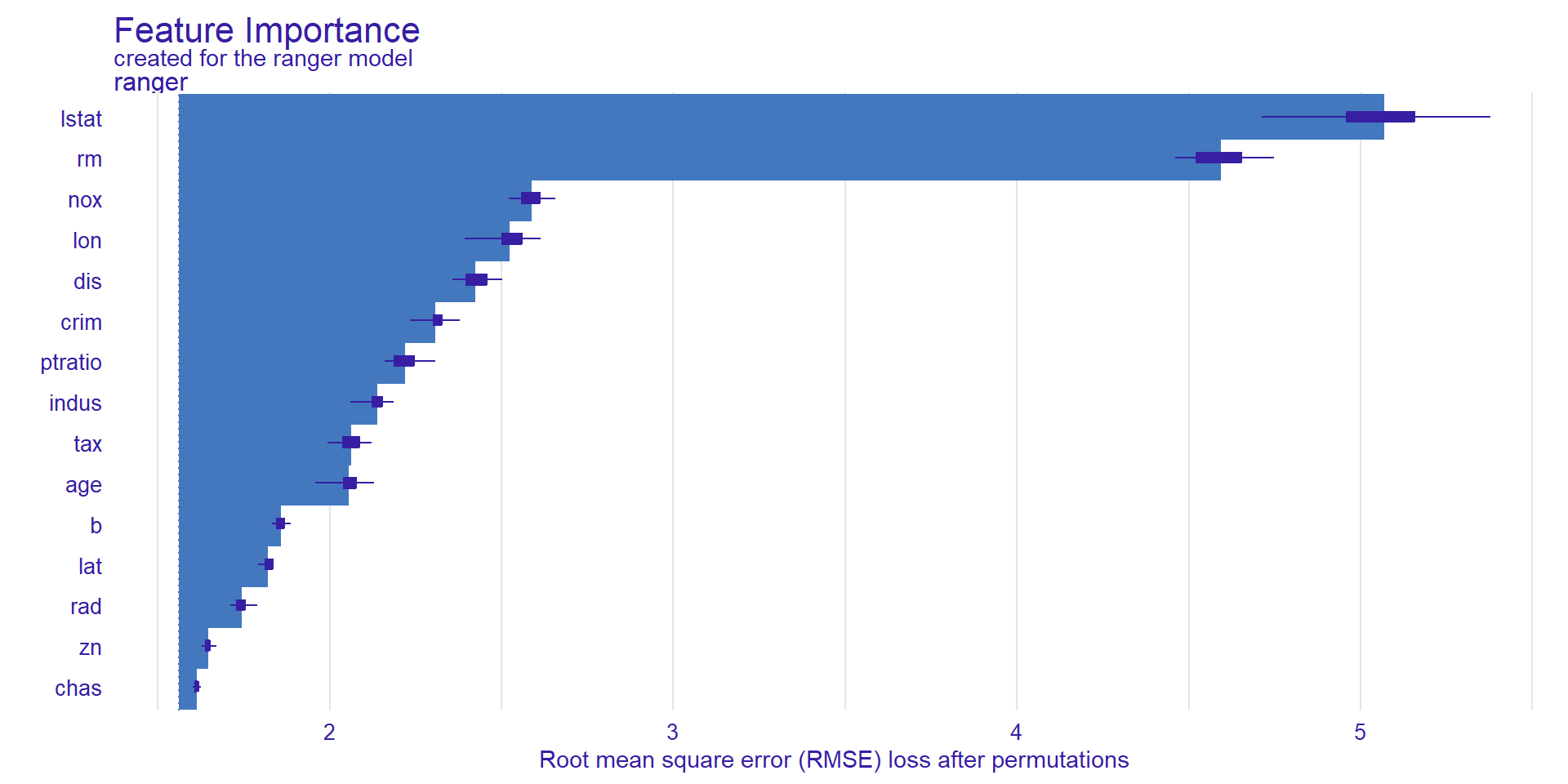
Partial dependence

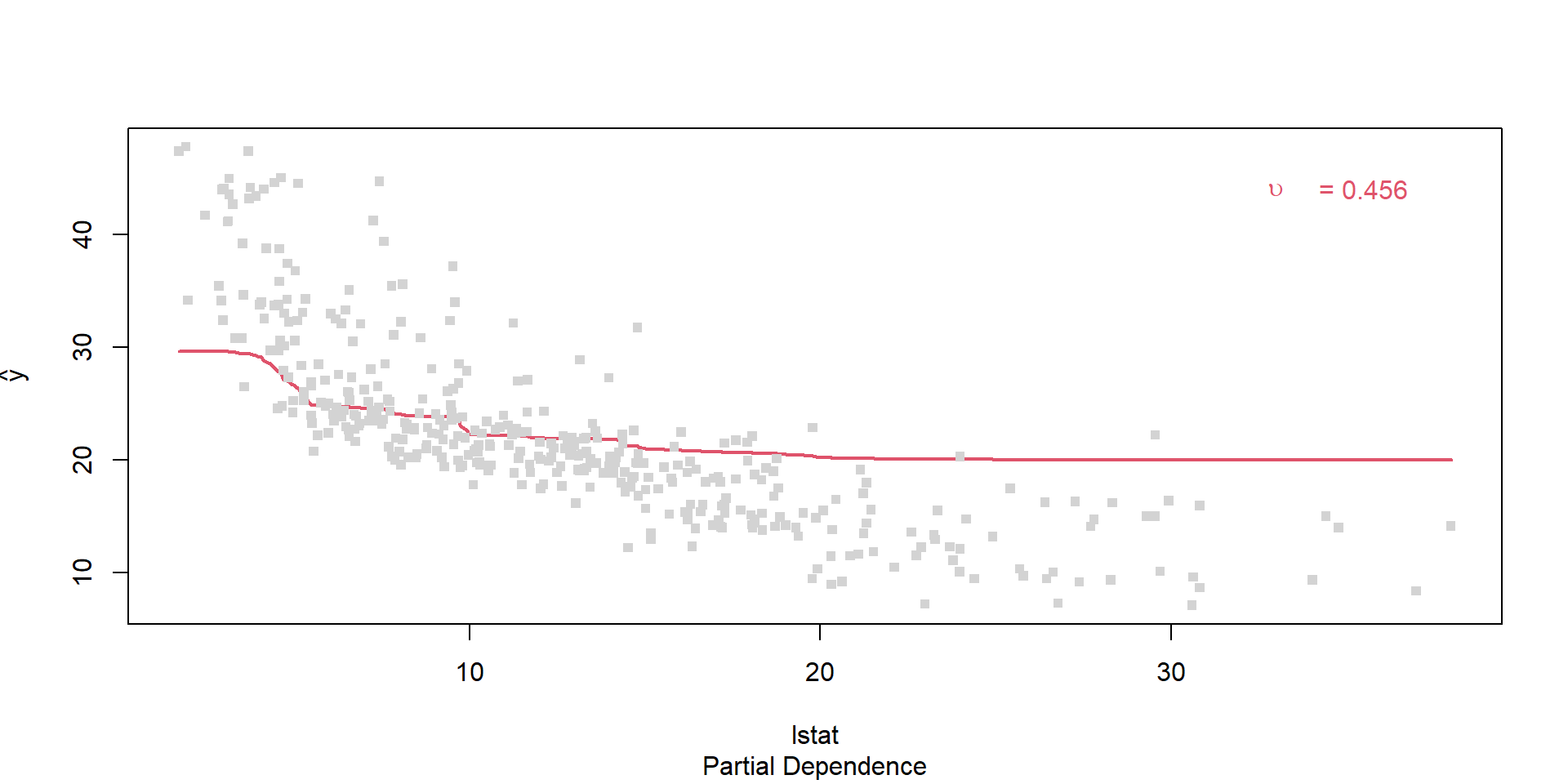
Explainability

Appropriateness of an explanation (\(XAI\)) can be assessed via explainability (Szepannek and Lübke 2023)

\[\upsilon = 1 - \frac{ESD(XAI)}{ESD(\emptyset)} < 1\]

with

\[ ESD(XAI) = \int (\hat{f}(X) - XAI(X))^2 \; d P(X) \].

Most Representative Tree

Select one tree (\(T_*\)) from a forest with minimum average distance to all other trees:

\[\begin{equation} T_* = \arg \min_{T_j} \frac{1}{N}\sum_k d(T_j, T_k) \end{equation}\]

with e.g. 

\[\begin{equation} d(T_j, T_k) = \frac{1}{n} \sum_{i=1}^n \left( \hat{y}_{T_j} - \hat{y}_{T_k} \right)^2 \end{equation}\]

or proportion of discordant pairs (Banerjee, Ding, and Noone 2012).

Explainability of MRTs…

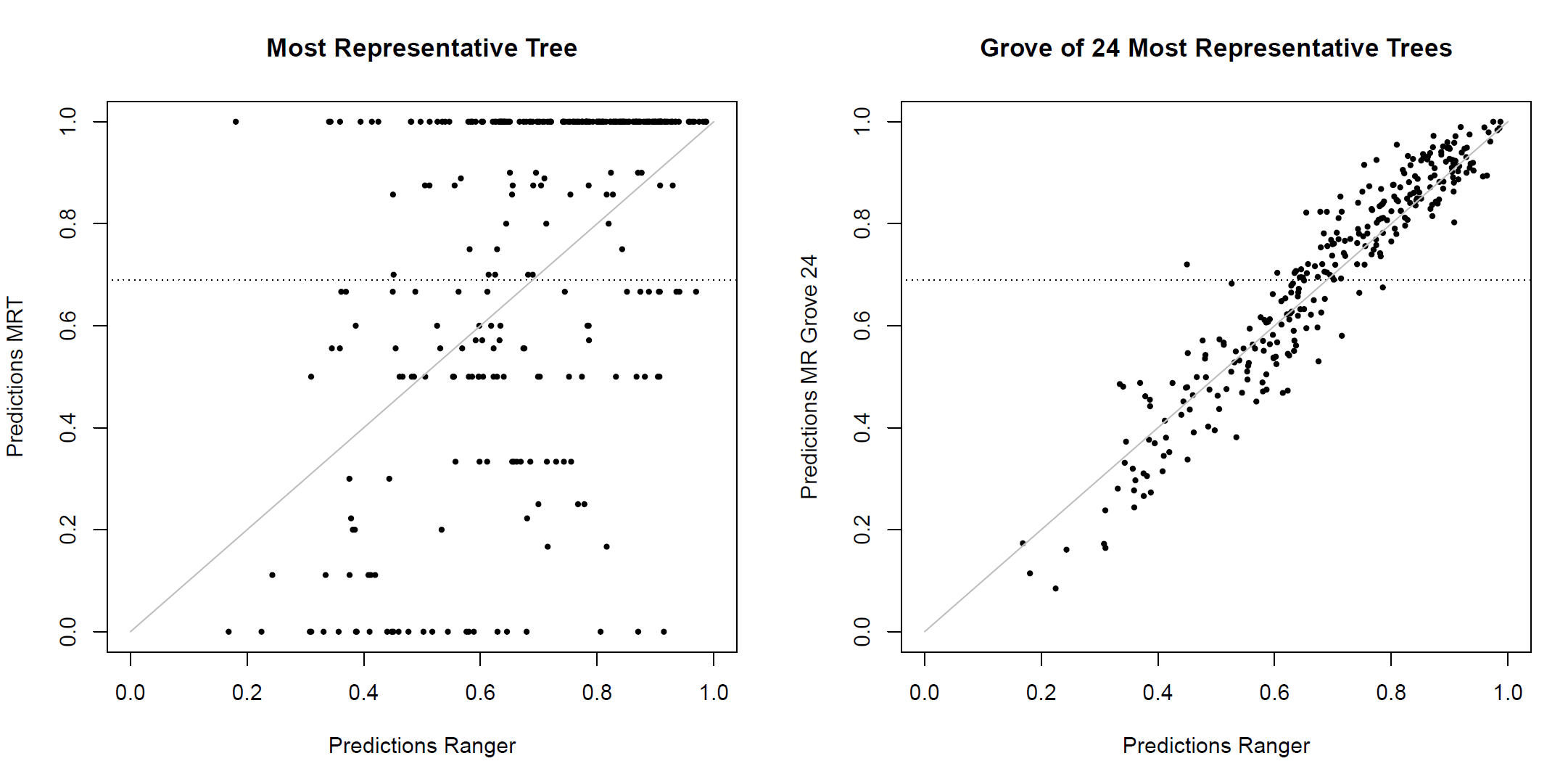
…Explainability of MRTs

Neither model agnostic, nor well suited, neither in terms of explainability nor in terms of complexity!

Trees	Rules	upsilon
1	80	<0
3	252	0.095
10	822	0.687
24	1944	0.871

(Szepannek and Laabs 2024)

Humans’ working memory capacity limited (Miller 1956; Cowan 2010).

Explanation Groves…

• Idea: Find optimal set of rules.
• Surrogate model (cf. e.g. Molnar 2022).
  
• Stagewise optimization of \(XAI^{(m)}(x)\):

\[\begin{eqnarray} & \left. -\frac{\partial ESD(XAI)}{\partial XAI(x_i)} \right\rvert_{XAI(x_i) = XAI^{(m-1)}(x_i)} \nonumber \\ = & \left. -\frac{\partial (\hat{f}(x_i) - XAI(x_i))^2}{\partial XAI(x_i)} \right\rvert_{XAI(x_i) = XAI^{(m-1)}(x_i)} \nonumber \\ = & \; 2(\hat{f}(x_i) - XAI^{(m-1)}(x_i)) \nonumber \\ = & :\tilde{y}_i \end{eqnarray}\]

• Unexplained residual represents target of next iteration.

Resulting Explanation

Structure of the resulting explanation:

\[\begin{eqnarray} XAI^{(m)}(x) & = & XAI^{(m-1)}(x) \nonumber \\ & & + \; \gamma_{m+} \; \mathbf{1}_{(x \in R^{(m)})} \nonumber \\ & & + \; \gamma_{m-} \; \mathbf{1}_{(x \notin R^{(m)})}. \end{eqnarray}\]

• \(\gamma_{m}\): Weights added at \(m^{th}\) iteration.
• \(R^{(m)}\): Rule added at \(m^{th}\) iteration.
• Note: Number of rules can be controlled by the number of iterations!

Rules to Explain the Random Forest

variable	upper_bound_left	levels_left	pleft	pright
Intercept	NA	NA	22.330	22.330
crim	14.143	NA	0.389	-5.041
dis	1.357	NA	5.250	-0.147
lon	-71.048	NA	0.762	-0.915
lstat	5.230	NA	3.320	-0.500
lstat	14.435	NA	2.490	-4.765
rm	6.812	NA	0.766	-3.482
rm	6.825	NA	-2.673	12.363
rm	7.437	NA	-0.266	4.639

Code Demo of R Implementation

# train model
library(ranger)
rf <- ranger(cmedv ~ ., data = train)


library(xgrove)

# define complexity of resulting explanations
ntrees <- c(4,8,16,32,64,128)

# remove target variable from data
pf     <- function(model, data) return(predict(model, data)$predictions)

# remove target variable from data
data   <- train[,-3] 

# explanation groves
xg <- xgrove(rf, data, ntrees, pfun = pf)

Illustration (Surrogate Rules)

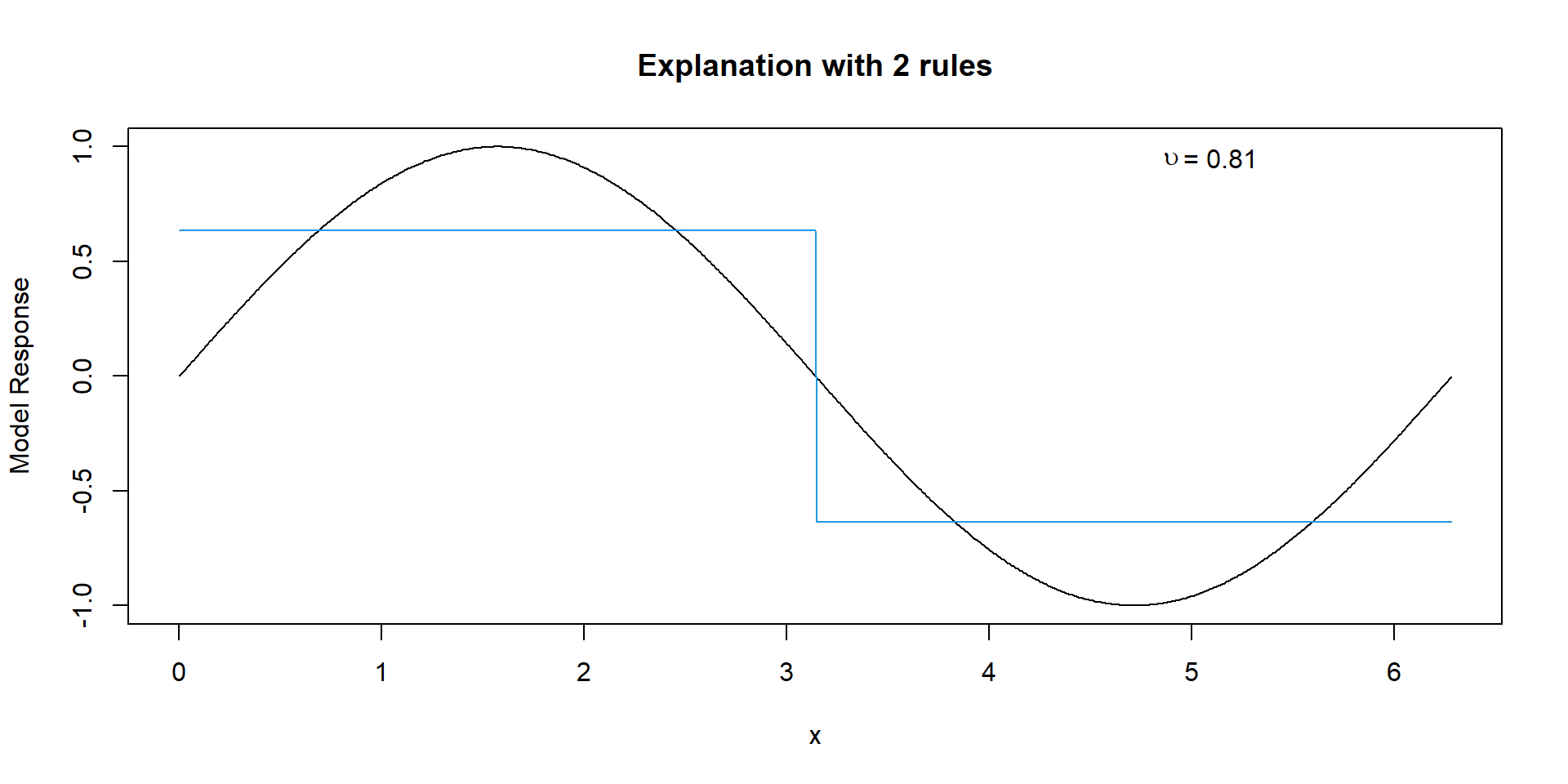
Explanation with 2 Rules

Explanation with 5 Rules

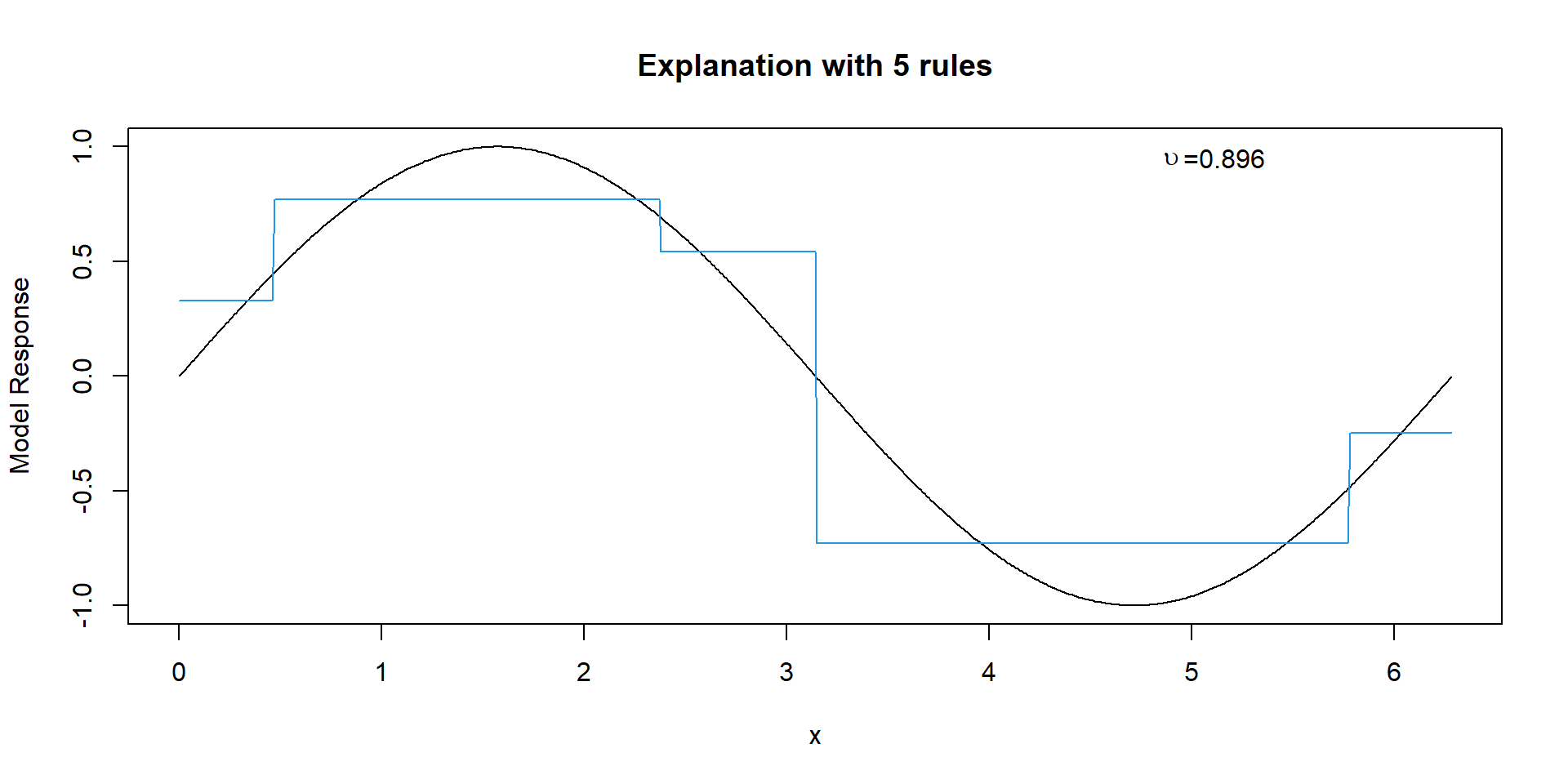
Explanation with 17 Rules

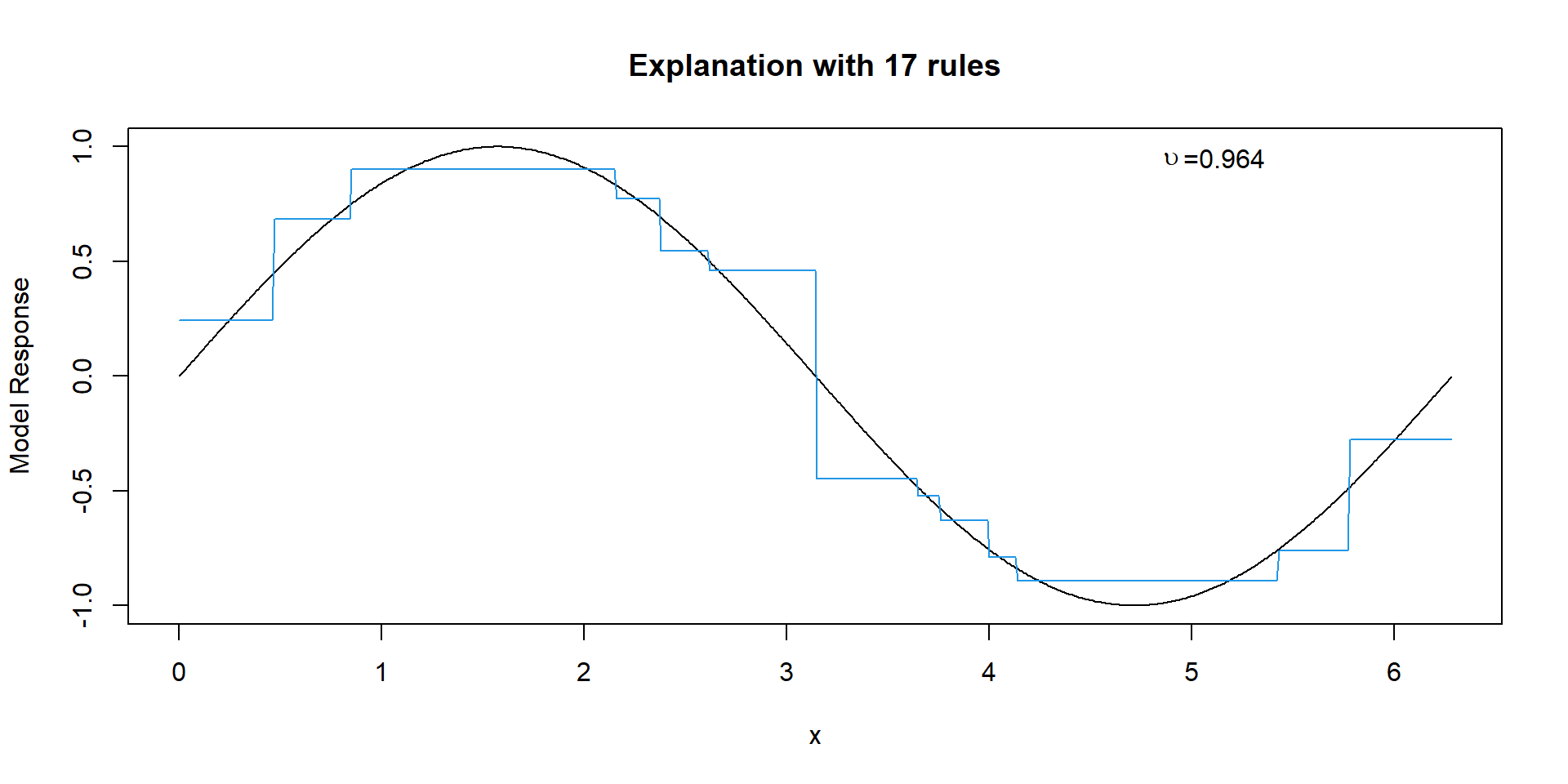
Explanation with 65 Rules

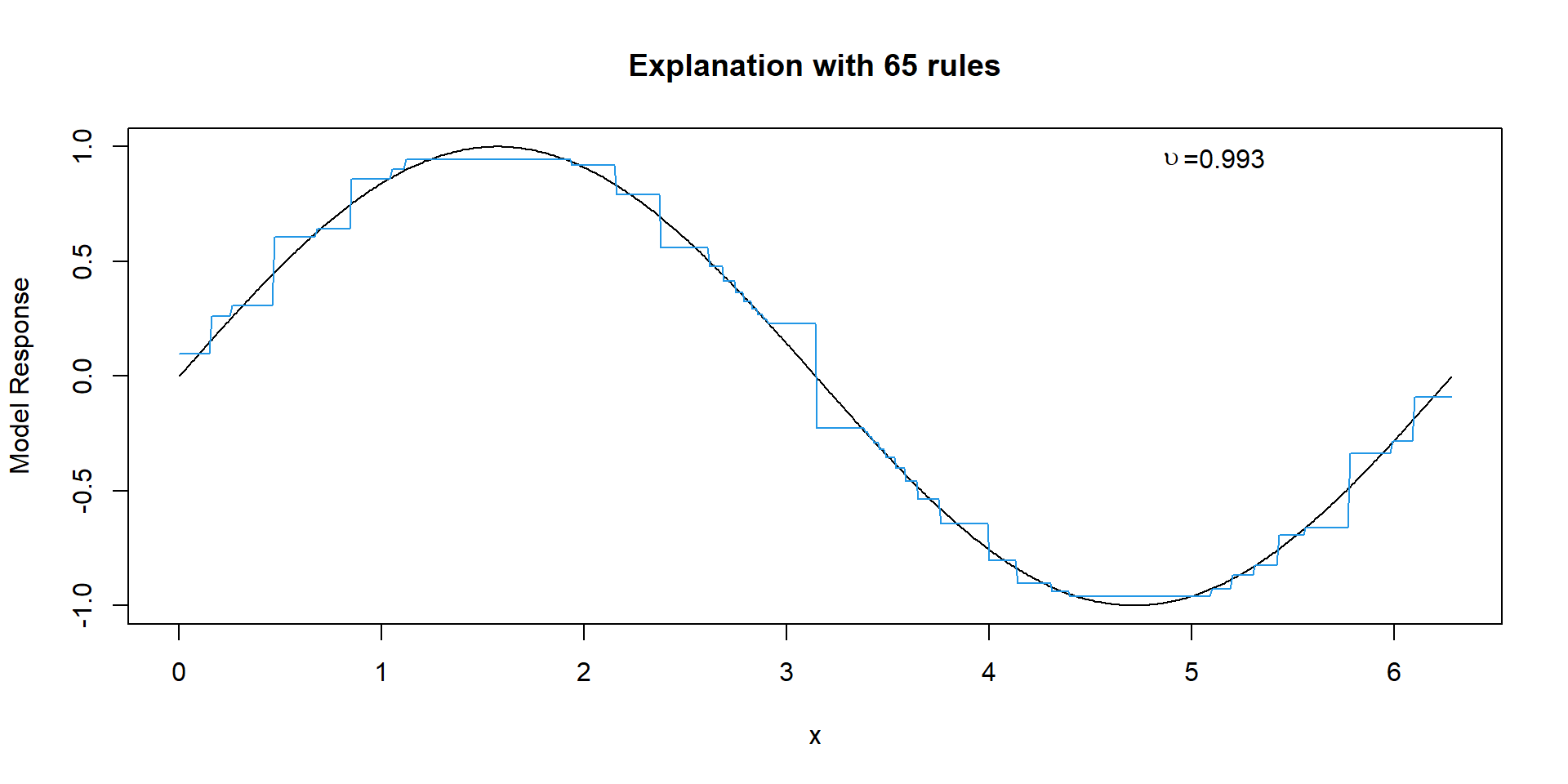
Trade-off for Boston Housing Data

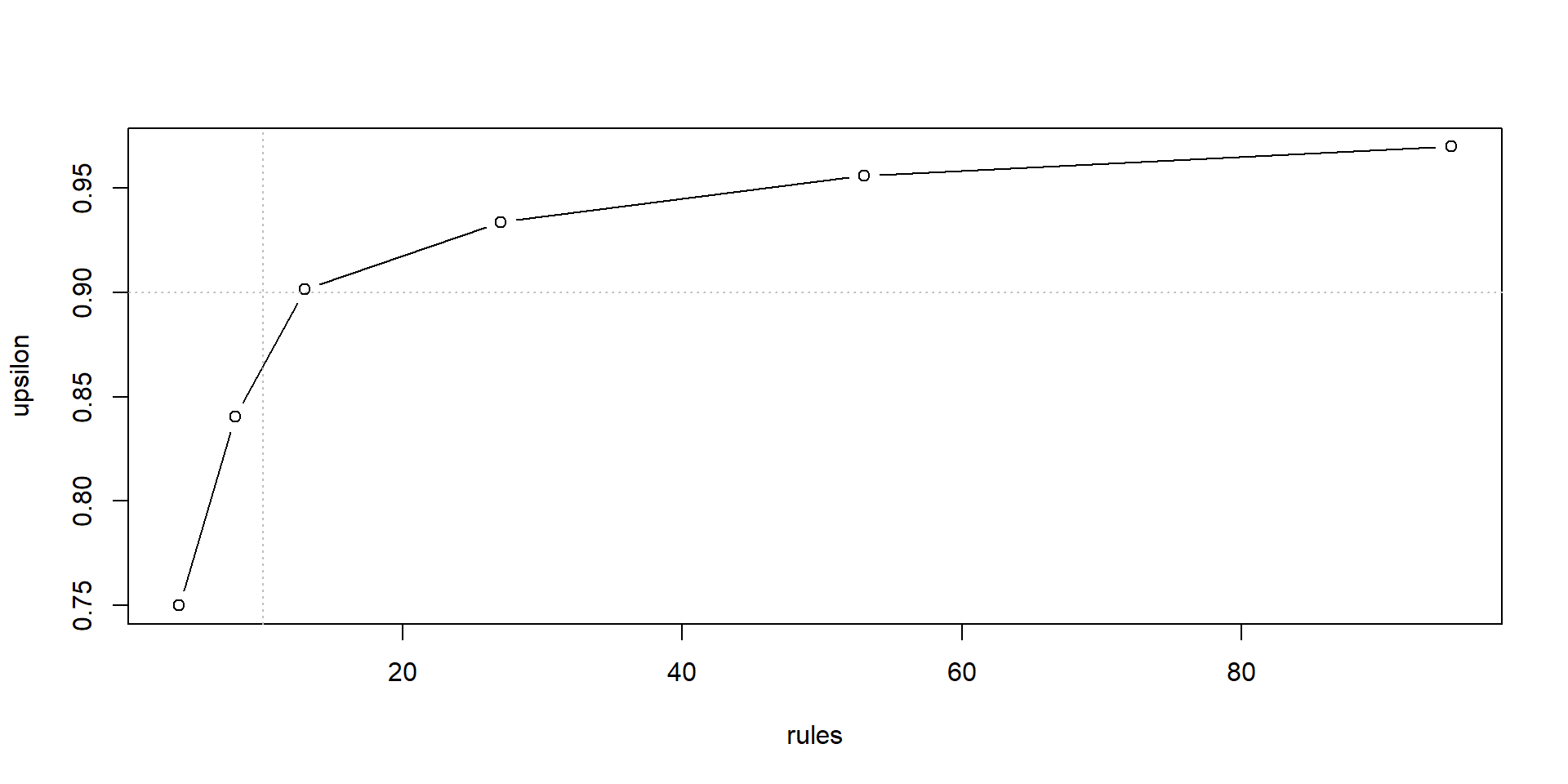
Simulation Study

Learners: - decision tree (rpart), - random forest (ranger), - neural network (nnet), - svm (e1071) and - xgboost (xgb)

77 Tasks: - 33 regression taks - and 34 binary classification tasks
- Nenchmark suites from OpenML data base (Bischl et al. 2021; Fischer, Feurer, and Bischl 2023).

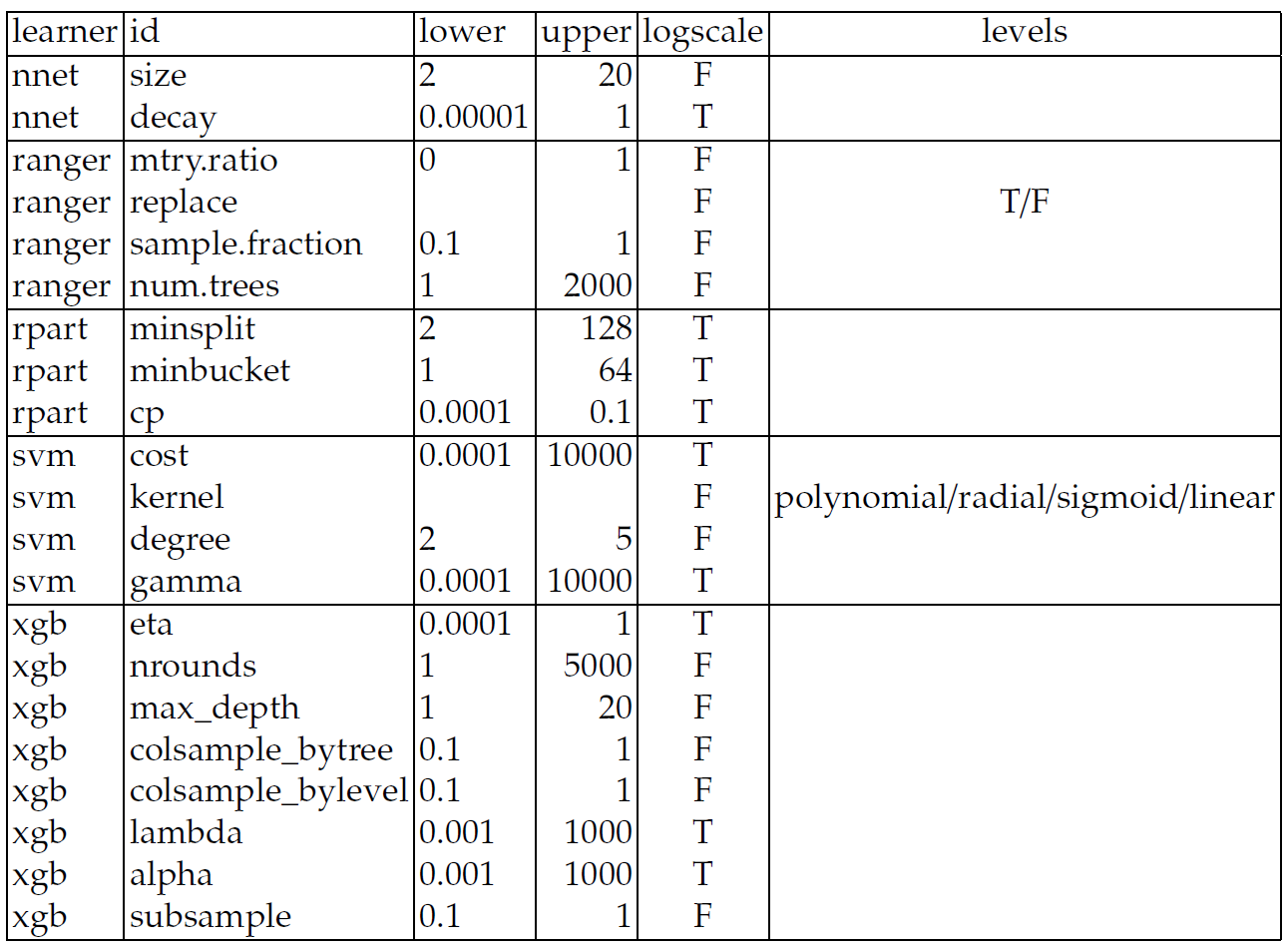
Hperparameter Tuning

• Goal: Find a reasonable parameter set, not necessarily the best,
• Random search \(n = 20\),
• Five-fold CV,
• Note: No separate test data (not scope).
• Final retraining on entire data,

Results

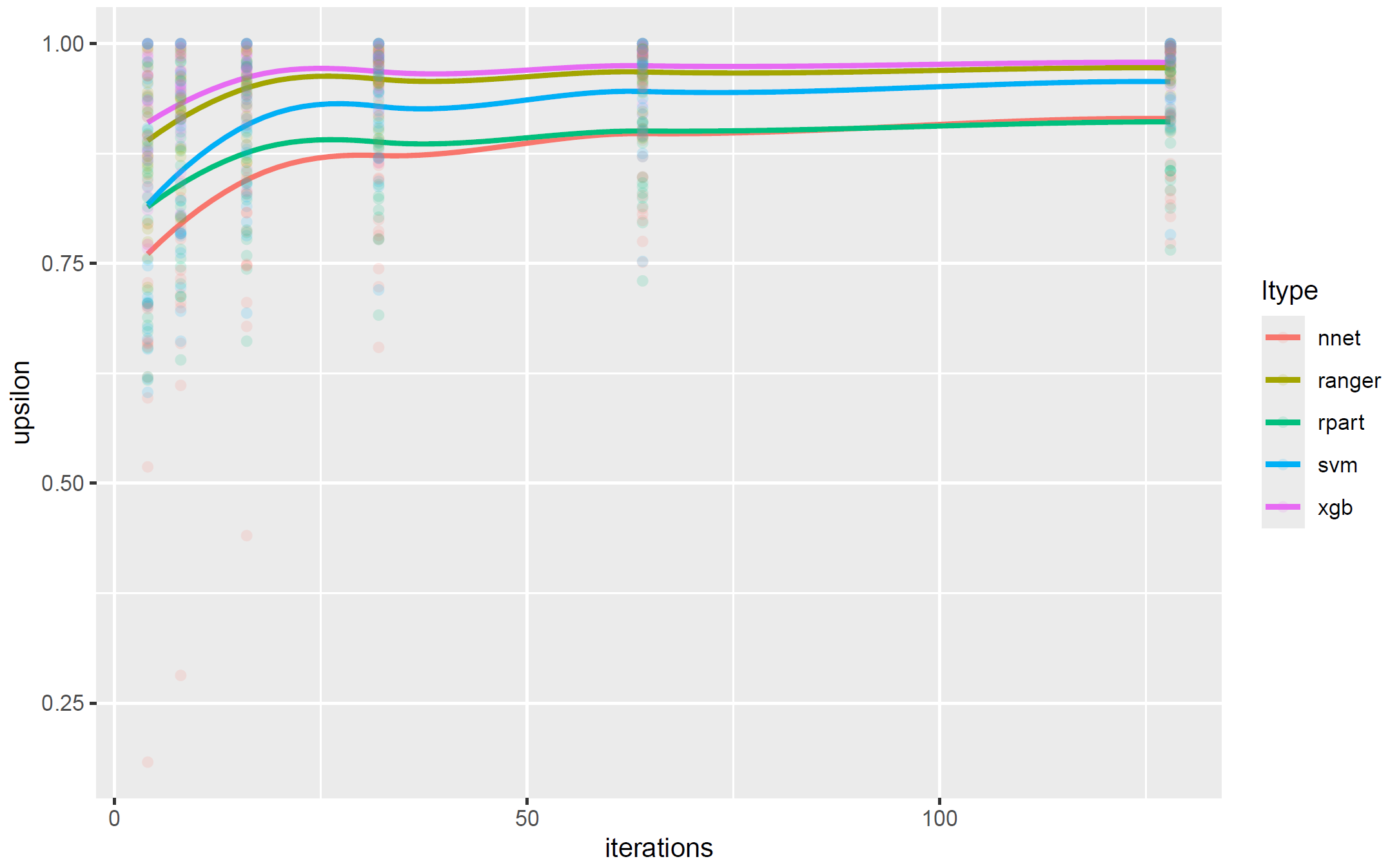
…Results

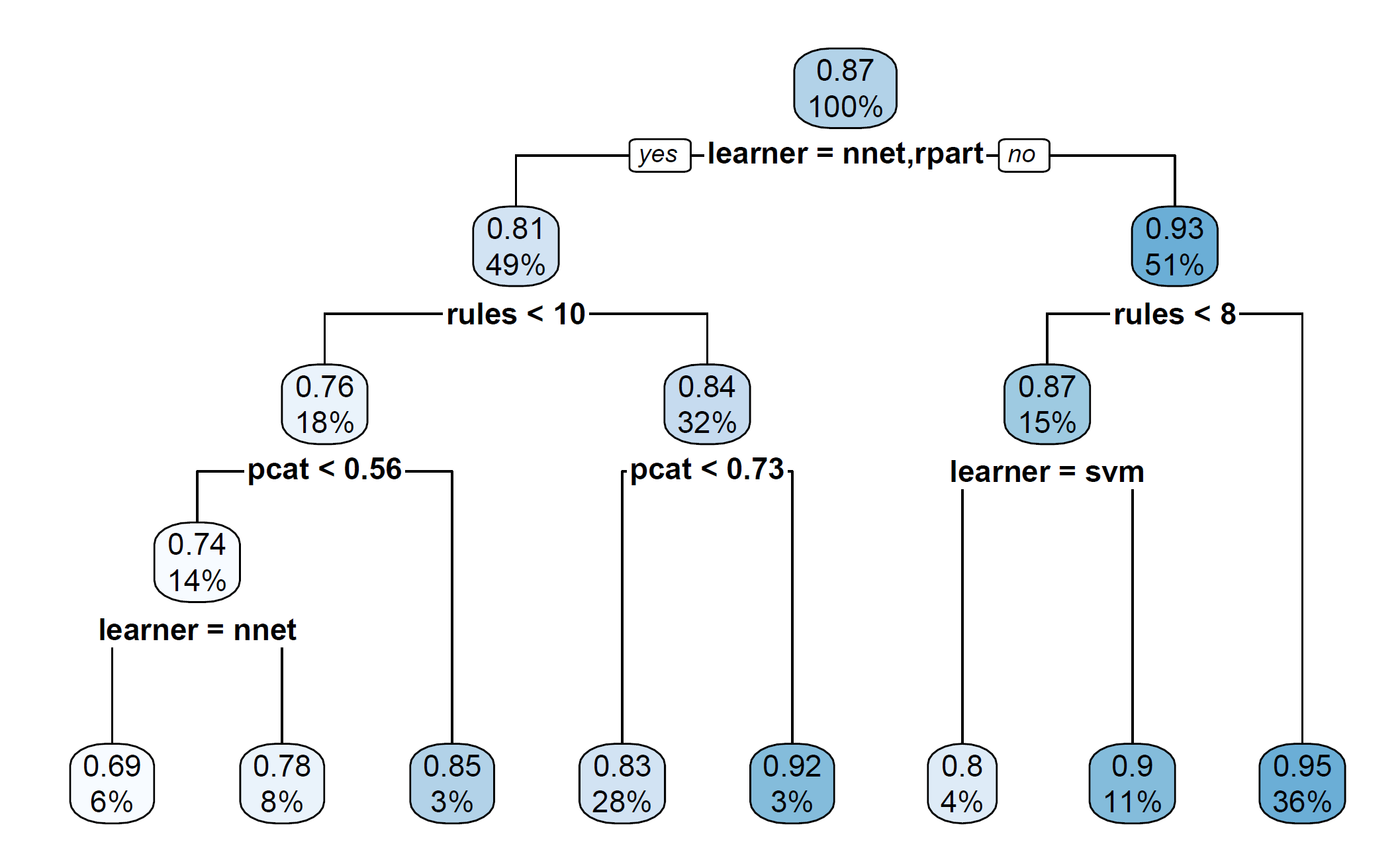
Summary

• Flexibility vs Interpretability
• Explanation Groves:
  • extract set of explainable rules that maximize explainability \(\upsilon\),
  • at the same time control complexity of the explanation,
  • analyze trade-off between complexity and adequacy of an explanation.
• (!) There does not necessarily exist an easy explanation of a complex model.
• Implementeted in the R package xgrove.

Available on CRAN.

ECDA & GPSDAA 2026

European Conference on Data Analysis 2026

German Polish Seminar on Data Analysis and Applications (GPSDAA)

on September \(11^{th}/12^{th}\) on the island of Hiddensee.

Thank You!

Banerjee, Mousumi, Ying Ding, and Anne-Michelle Noone. 2012. “Identifying Representative Trees from Ensembles.” Stat Med 31 (15): 1601–16. https://doi.org/10.1002/sim.4492.

Bischl, Bernd, Giuseppe Casalicchio, Matthias Feurer, Pieter Gijsbers, Frank Hutter, Michel Lang, Rafael Gomes Mantovani, Jan N. van Rijn, and Joaquin Vanschoren. 2021. “OpenML Benchmarking Suites.” In Thirty-Fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2). https://openreview.net/forum?id=OCrD8ycKjG.

Breiman, Leo. 2001. “Statistical Modeling: The Two Cultures.” Statist. Sci. 16 (3): 199–231. https://doi.org/10.1214/ss/1009213726.

Bücker, Michael, Gero Szepannek, Alicja Gosiewska, and Przemyslaw Biecek. 2021. “TAX4CS – Transparency, Auditability and eXplainability of Machine Learning Models in Credit Scoring.” Journal of the Operational Research Society, 1–21. https://doi.org/10.1080/01605682.2021.1922098.

Cowan, Nelson. 2010. “The Magical Mystery Four: How Is Working Memory Capacity Limited, and Why?” Curr Dir Psychol Sci 19 (1): 51–57. https://doi.org/10.1177/0963721409359277.

European Commission. 2024. “EU Artificial Intelligence Act.” https://artificialintelligenceact.eu/the-act/.

Fernández-Delgado, Manuel, Eva Cernadas, Senén Barro, and Dinani Amorim. 2014. “Do We Need Hundreds of Classifiers to Solve Real World Classification Problems?” J. Mach. Learn. Res. 15 (1): 3133–81.

Fischer, Sebastian Felix, Matthias Feurer, and Bernd Bischl. 2023. “OpenML-CTR23 a Curated Tabular Regression Benchmarking Suite.” In AutoML Conference 2023 (Workshop). https://openreview.net/forum?id=HebAOoMm94.

Gosiewska, Alicja, and Przemyslaw Biecek. 2019. “Do Not Trust Additive Explanationss.” https://arxiv.org/pdf/1903.11420.

Harrison, D., and D. L. Rubinfeld. 1978. “Hedonic Prices and the Demand for Clean Air.” J. Of Environmental Economics and Managemen 5: 81–102.

James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2019. An Introduction to Statistical Learning. Second Edition. Springer.

Miller, George. 1956. “The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information.” Psychological Review 63 (2): 81–97. https://doi.org/10.1037/h0043158.

Molnar, Christoph. 2022. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable. 2nd ed. https://christophm.github.io/interpretable-ml-book.

Molnar, Christoph, Gunnar König, Julia Herbinger, Timo Freiesleben, Susanne Dandl, Christian A. Scholbeck, Giuseppe Casalicchio, Moritz Grosse-Wentrup, and Bernd Bischl. 2022. “General Pitfalls of Model-Agnostic Interpretation Methods for Machine Learning Models.” In xxAI - Beyond Explainable AI: Int. Workshop at ICML 2020, edited by Andreas Holzinger, Randy Goebel, Ruth Fong, Taesup Moon, Klaus-Robert Müller, and Wojciech Samek. Springer. https://doi.org/10.1007/978-3-031-04083-2_4.

Probst, Philipp, Anne-Laure Boulesteix, and Bernd Bischl. 2021. “Tunability: Importance of Hyperparameters of Machine Learning Algorithms.” J. Mach. Learn. Res. 20 (1): 1934–65.

Rudin, Cynthia. 2019. Stop Explaining Black Box Machine Learning Models for High Stakes Decisions and Use Interpretable Models Instead. https://arxiv.org/abs/1811.10154.

Szepannek, Gero. 2017. “On the Practical Relevance of Modern Machine Learning Algorithms for Credit Scoring Applications.” WIAS Report Series 29: 88–96. https://doi.org/10.20347/wias.report.29.

Szepannek, Gero, and Björn-Hergen Laabs. 2024. “Can’t See the Forest for the Trees.” Behaviormetrika 51: 411–23. https://doi.org/10.1007/s41237-023-00205-2.

Szepannek, Gero, and Karsten Lübke. 2022. “Explaining Artificial Intelligence with Care.” KI - Künstliche Intelligenz. https://doi.org/10.1007/s13218-022-00764-8.

———. 2023. “How Much Do We See? On the Explainability of Partial Dependence Plots for Credit Risk Scoring.” Argumenta Oeconomica 50. https://doi.org/10.15611/aoe.2023.1.07.

Therneau, Terry M., and Elizabeth J. Atkinson. 2015. “An Introduction to Recursive Partitioning Using the RPART Routines.” In. https://www.biostat.wisc.edu/~kbroman/teaching/statgen/2004/refs/therneau.pdf.

Woźnica, Katarzyna, Katarzyna Pękala, Hubert Baniecki, Wojciech Kretowicz, Elżbieta Sienkiewicz, and Przemysław Biecek. 2021. “Do Not Explain Without Context: Addressing the Blind Spot of Model Explanations.” https://arxiv.org/pdf/2105.13787.

Wright, Marvin N., and Andreas Ziegler. 2017. “Ranger: A Fast Implementation of Random Forests for High Dimensional Data in c++ and r.” Journal of Statistical Software 77 (1): 1–17. https://doi.org/10.18637/jss.v077.i01.